
안녕하세요 주엉입니다 ღ'ᴗ'ღ
오늘도 음정에 대한 추가적인 설명을 들고왔습니다.
바로 겹음정,복음정에 관한이야기인데요!
둘은 같은의미입니다. (복 = 겹칠 복)
저번 음정 첫시간에 했던 내용들은 홑음정 이라고도 합니다.
Simple interval 이라고도 합니다. 8도 이내의 음정관계라고 이해하면되겠습니다.
겹음정,복음정 (Compound interval )
- 한 옥타브가 넘는 두 음사이의 관계
오늘은 한 옥타브가 넘는 두개의 음 사이의 거리를 계산해보도록 할게요~!
문제풀이 방법은 간단합니다 ! 홑음정으로 (지난시간 음정 계산방법) 계산한뒤 도수에 7을 더해주면 끝입니다!
예를 들어 아래 문제를 볼까요?
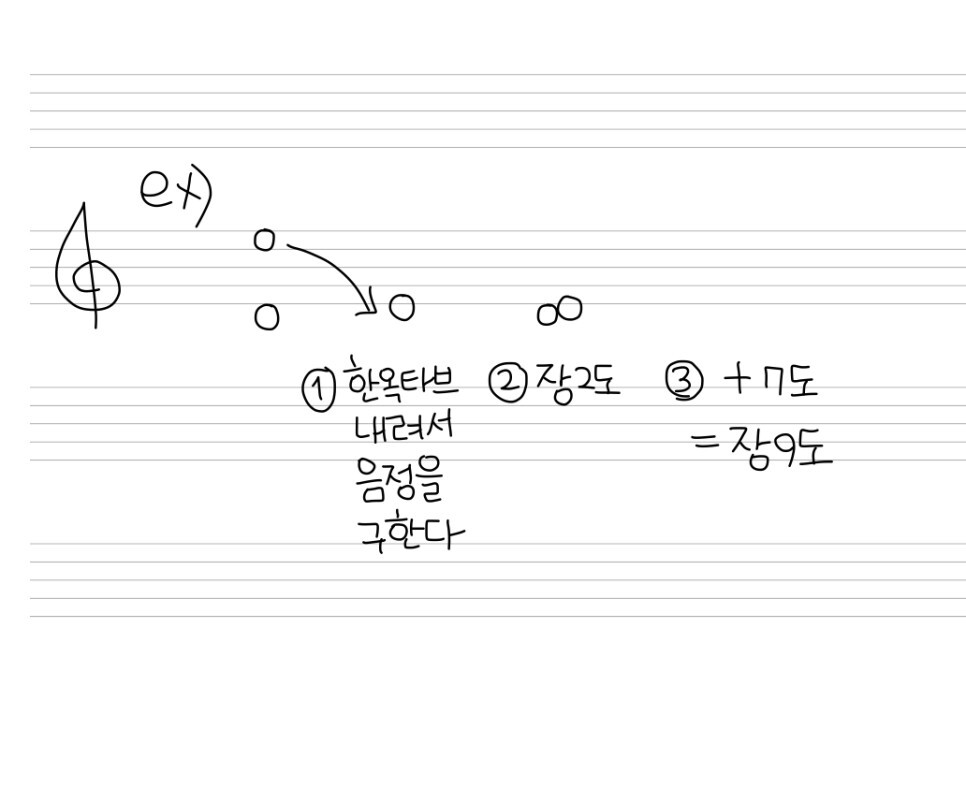
위에 적혀있는 순서대로 음정 관계를 구하시면됩니다 . 아주 쉽죵?
나중에 Tension (9,11,13도)이라는 것을 공부하게 될때가 올텐데 그때를 대비해서라도 미리 한옥타브 이상의 음관계에 있어서
미리 익숙하게 된다면 도움이 많이 될것입니당!
----------------------------------------------------------------------------------------------------------------------
다음은 자리바꿈 음정에 관한 이야기를 해볼게요~!
자리바꿈음정 (Inversion Interval) - 음정에서 위아래 자리를 바꾸는것
자리바꿈은 전위라고도 하고 영어로는 Inversion 이라고도 합니다.
말그대로 두개의 음을 자리바꿈 한게 자리바꿈 음정입니다~!
자리바꿈음정 계산법도 어렵지가않으니 같이 계산해볼까요?
아래의 예시를 봐주세용
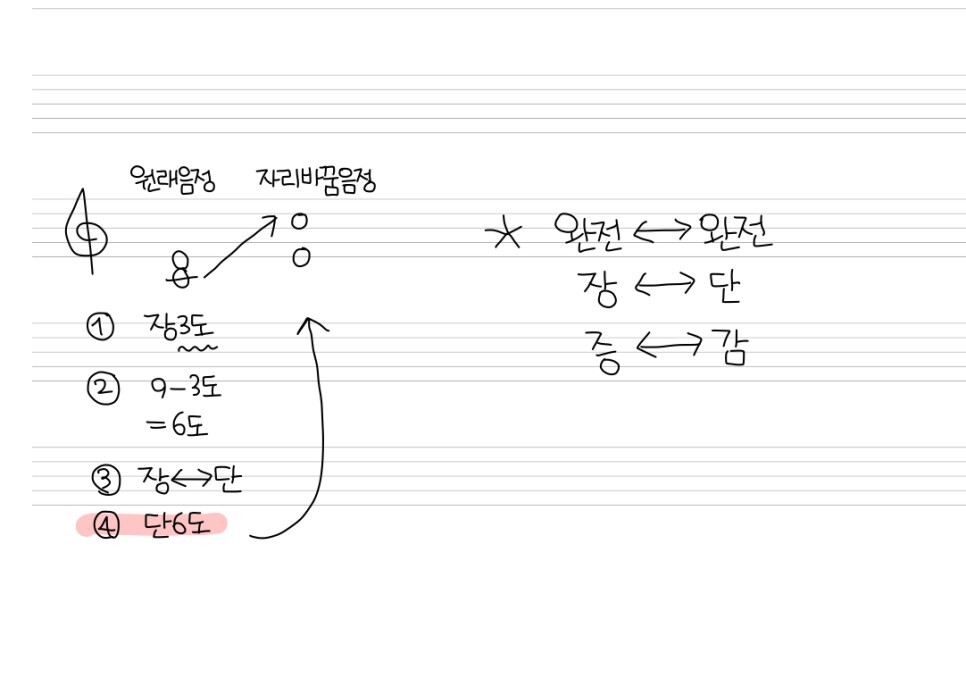
1. 원래 음정 관계를 구한다
2. 9에서 원래 음정 도수(3도) 를 뺀다 =6도
3. 원래 도수앞의 이름이 어떤 것이냐에 따라 자리바꿈음정의 이름도 바뀐다. (오른쪽 관계 참고)
4. 장은 단과 바뀐다는것을 알수있으니, 결국 단6도가 자리바꿈음정의 답!
- 이런 순서로 계산해도되고, 그냥 자리바꿈음정을 보고 구하셔도됩니다.
여기서 저는 개인적으로 놀란부분이있었는데요.
저번시간에 배운 완전어울림음정/불완전어울림음정/안어울림음정 과 관계가 있다는점입니다!!

다시 가져와봤어용 여러분들과 이 놀라운사실을 같이 공유하고자,,ㅎ_ㅎ
예를들어 9-원래음정 도수 (1) 일때 = 8이되죠. 둘다 완전어울림음정에 속한 관계입니다.
9-4를 하면 5도가 되는데 이것 또한 4,5도가 둘다 완전어울림음정에 속해요.
이런식으로 다른 음정들도 계산해보면 도수도, 이름도 마찬가지로 하나의 음정어울림 속에 속한다는 사실입니다!!
너무 놀랍지않나여 저는 이 사실을 깨닫고 마치 수학처럼 딱딱 맞춰지는것이,, 쾌감이 느껴졌어요,,ㅎ_ㅎ
화성학을 만든 분 진짜 존경,,소름,,
코드를 자리바꿈(전위,Inversion) 해서 많이 연주됩니다.
저는 자리바꿈된 코드들을 마치 꽃 같다고 표현하는데요
그만큼 굉장히 연주하는 부분에있어서는 중요하다고 생각합니다. 가까운 자리로 이동하며 코드의 진행에있어서 연결이 자연스럽게 해주는 역할을 하기때문이죠 :)
어쨌든 코드의 자리바꿈하는 상황에있어서도 기본적인 개념은 바로 이 자리바꿈음정이기때문에
이부분을 잘 이해해놓으면 코드의 자리바꿈에서도 잘 이해할수있고, 도움이 많이 될거라 생각합니다.
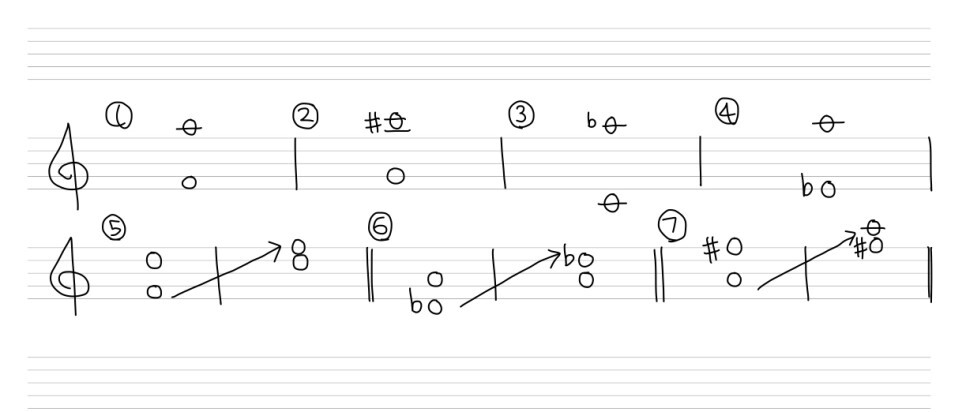
몇개의 문제를 올려놓을테니 한번 풀어보세요!!

댓글